In Houdini, there are several ways to manipulate how an object moves within a solver or DOP network:

Direct Position Modification #

The first thing that comes to mind is to add some vector to a position like so:

vector v = set(1,0,0);
v@P += v;

While this directly sets the position, it can lead to problems. It changes the position without considering the real units - meters per second. This method has lots of issues:

• If the object is already moving, this method abruptly overrides its current position.
• This can cause jerky, unrealistic motion.
• It also ignores the object’s mass, making it harder to predict how different objects will react.
• This approach doesn’t account for the object’s velocity or acceleration, making it less realistic.

Position Modification with Time Increment #

vector v = set(1,0,0);
v@P += v * @Timeinc;

Let’s try and improve it by multiplying the vector by @Timeinc (the length of the current step, usually 1 frame length or 1/$FPS) ensures a consistent result regardless of the frame rate or subframe stepping. It allows us to move the point in meters per second. However, it still lacks the consideration of forces and mass, which are crucial for realistic simulations.

Finally Using Forces #

vector force = {1,0,0};
v@v += force * @Timeinc;
v@P += v@v * @Timeinc;

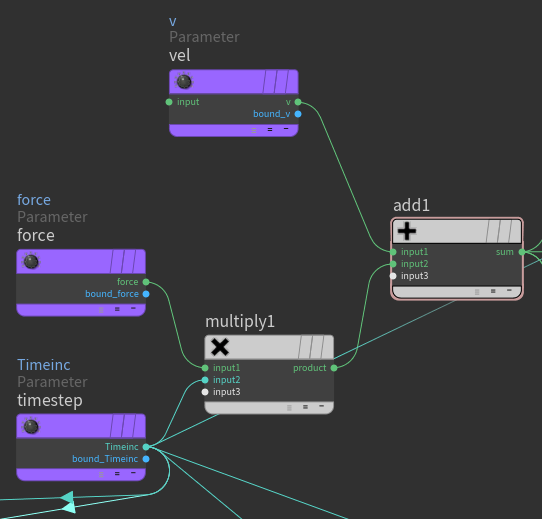
In this method, the force (acceleration) applied to the object determines the velocity over time. (in pop network it also uses various drag and mass forces internally) According to the Newton’s Second Law of Motion. The velocity, in turn, changes the position over time.

The logical flow is: force -> v (velocity) -> P (position)

// Force is an acceleration (or deceleration)
vector force = @force;

// Calculate acceleration (a = F / m)
vector acceleration = force / mass;

// Update velocity (v += a * dt)
@v += acceleration * @TimeInc;

// Update position (P += v * dt)
@P += @v * @TimeInc;

[! info] When you set a force, it continuously alters the object’s velocity, which then updates the object’s position. For instance, an object with an initial velocity of {0,1,0} will move one Houdini unit upwards in one second. The actual movement per frame depends on the scene’s frame rate. For example, at 25 FPS, the object will move 1/25th of its velocity per frame.

[! info] When manipulating @v (velocity) in wrangles or VOPs, always incorporate @Timeinc to normalize your velocities. (the length of the current step, usually 1 frame length or 1/$FPS). This ensures consistency across different frame rates and subframe steps: v@P += v@v * @Timeinc;

The logic in the pop solver, as you can see they apply force to the velocity